• Conservative surface wave effects on a wind-driven coastal upwelling system

  • Wave streaming effects on nearshore submesoscale currents

    Surface gravity waves are subject to bottom drag in shallow water. The bottom drag causes fluctuations to wave orbital velocities. After a wave phase average, the wave velocity fluctuations yield a stress that is able to drive a bottom Eulerian current along the direction of wave propagation. This bottom Eulerian current is called wave (bottom) streaming. The wave streaming is able to drive a Lagrangian overturing circulation in the inner shelf (Fig. 1a). A Lagrangian current is the sum of an Eulerian current and Stokes drift. When stratification is included, the wave streaming further induces a nearshore front (Fig. 2d) associated with the inner-shelf Lagrangian overturing circulation (Fig. 2b)

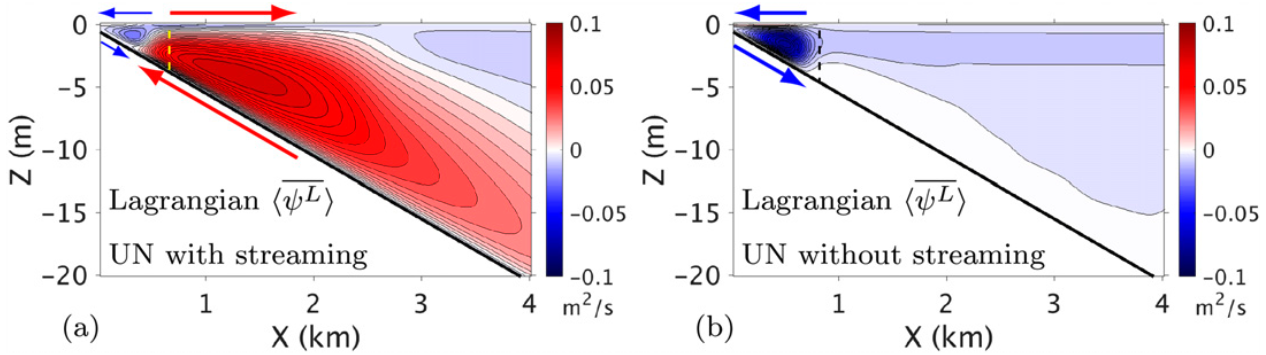
    image missing
    Figure 1. Lagrangian streamfunction defined in the cross-section (x-z) plane, (a) with wave streaming and (b) without wave streaming. The arrows indicate directions of Lagrangian currents. The dashed lines mark the surf-zone edge. Here the water is unstratified, in comparison to Fig. 2b with stratification.

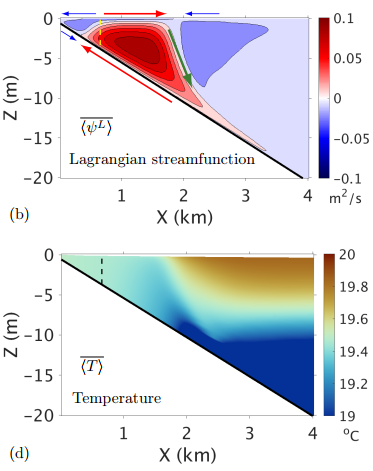
    image missing
    Figure 2. Wave streaming-induced (b) Lagrangian streamfunction and (d) front in stratified water. The arrows in (b) indicate directions of Lagrangian currents. The dashed lines mark the surf-zone edge.

    References:

    1. Wang*, P., McWilliams, J. C., Uchiyama, Y., Chekroun, M., Yi, D. L., 2020. Effects of wave streaming and wave variations on nearshore wave-driven circulation. Journal of Physical Oceanography, https://doi.org/10.1175/JPO-D-19-0304.1.

    2. Wang*, P., McWilliams, J. C, Uchiyama, Y., 2021. A nearshore oceanic front induced by wave streaming. Journal of Physical Oceanography, https://doi.org/10.1175/JPO-D-21-0004.1.

  • Langmuir circulation with phase-resolved surface gravity waves

    Explicit surface waves are modeled by a moving-mesh model; the domain's upper boundary undulates as waves. Langmuir number La = 0.4, wind stress 0.33N/m^2, wave amplitude 0.8m, wave length 45m, and wave period 6s. Domain size is 628m,314m,100m in the x,y,z directions. ( Bilibili or Youtube )

    References:

    Wang, P. , Özgökmen, T. M., 2018. Langmuir circulation with explicit surface waves from moving-mesh modelling. Geophysical Research Letters, https://doi.org/10.1002/2017GL076009. (PDF)

  • Spiral inertial waves emitted from an unstable oceanic eddy

    Cylindrical domain with Radius = 4 and Height = 1. Homogeneous fluid density. (Case rc216-5)

    1. Vertical vorticity evolutions of an initially-unstable vortex (Youtube video)

    2. Vertical velocity evolutions of an initially-unstable vortex, demonstrating (spiral) inertial waves (Youtube video)

    References:

    Wang, P., Özgökmen, T. M., 2016. Spiral inertial waves emitted from geophysical vortices. Ocean Modelling, https://doi.org/10.1016/j.ocemod.2016.01.001. (PDF)

  • 3D material transport inside an unstable oceanic eddy

    Cylindrical domain with Radius = 2 and Height = 1. Initially, a small patch of tracer is released in the center of a vortex at mid-depth.

    1. Case rc216-5s: evolutions of passive tracer in a initially-stable vortex (Youtube video).

    2. Case rc216-5: evolutions of passive tracer in an initially-unstable vortex (Youtube video).

    References:

    Wang, P., Özgökmen, T. M., 2015. How do hydrodynamic instabilities affect 3D transport in geophysical vortices? Ocean Modelling, https://doi.org/10.1016/j.ocemod.2015.01.002. (PDF)

  • Mixing inside an oceanic eddy

    Cylindrical domain with Radius = 1 and Height = 1.

    1. Case rc175: homogeneous density, larminar fluid, stable vortex (Youtube video)

    2. Case rcd18-3: stratified density, turbulent fluid, unstable vortex (Youtube video)

    References:

    1. Pratt, L. J., Rypina, I. I., Özgökmen, T. M., Wang, P., Childs, H., Bebieva, Y., 2014. Chaotic advection in a steady, three-dimensional, Ekman-driven eddy. Journal of Fluid Mechanics, https://doi.org/10.1017/jfm.2013.583. (PDF)
    2. Rypina, I., Pratt, L. J., Wang, P., Özgökmen, T. M., Mezić, I., 2015. Resonance phenomena in 3D time-dependent volume-preserving flows with symmetries. Chaos, https://doi.org/10.1063/1.4916086. (PDF)